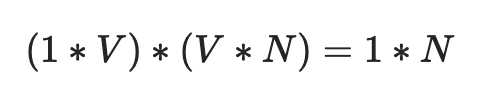All you need to know about the word2vec vectorisation

Big time bugbear for data science community while training a machine learning model is curating meaningful numerical data from the contrasting input data.

Feb 01, 2023

Converting any form of data into numerical data has been an all time. headache in the machine learning community. In NLP alone there has been extensive research in the field of vectorising the natural language into numerical data. In this series of complete NLP blog series, let's do a deep dive into word2vec models and their variants.

Agenda for the article is to discuss how the word2vec model works and see how to implement it.

But why word2vec model?

In 2013, Google introduced word2vec model that took the NLP world for a storm 🌪️. Unlike the TF-IDF and Bag of words model, the most important aspect of word2vec model was, for the first time, vectorising a word considered the semantic outlook 😎. The basic overview of word2vec model was to convert each word of a sentence into vectors using a neural network. By semantic outlook, I meant that two words which are similar in meaning will be closer to each other in the vector space. The most in fashion example to describe this is:

king - man + woman = queen

some of the important characteristics of this model are:

Preserve relationships between the words
Deals with the addition of new words in the vocabulary
Better results in lots of deep learning application

There are mainly two models which are pretty standards in the NLP industry:

Skip-Gram model

Super superficially telling “this shallow neural network predicts the context of the input word”.

hmm that seems to take away the need to go through the blog post

This simple shallow neural network consists of an input layer, a hidden and an output layer. It takes a word of the current sentence(wi) as the input and outputs the words before and after the sentence. Which is simply the context of the word. For example if we have a vocabulary of 10000 words, it predicts between which words in the vocabulary the word can be placed.

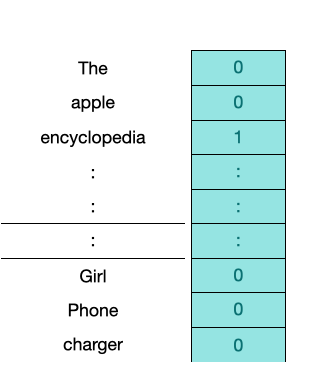
But how the word to be given as input. The answer is one-hot encoding. ̛Its simple as putting a 1 in at the place of 10000 sized vectors with all elements as 0s.

Let's say one-hot encoding for the word ‘encyclopedia’ in a corpus of 10000 words will look something like this:

Fig1: one-hot encoding for encyclopedia in a 10000 word vocabulary would look like this

Lets see how the model works. The model takes in a word pass in through the hidden layer, lets say 300 neurons(as used by the Google). And the output layer, which has 10000 neurons, predicts each word's probability, representing each word. The values in the vectors of 10000 length having the highest score will be the neighbouring words to the current word. It means lets say, wi is the current word, the model will be giving be higher score to the words which would be neighbouring to the current word.

\(w_{i-1}, w_{i-2}, w_{i+1}, w_{i+2}\)

The elements in the output vector are the predicted neighbouring words for the current input word wi.

But the interesting thing is that, its not the output of this trained model, we are taking as the embeddings but the hidden layer weights which is a vector of size 300. No activation function is applied on this hidden layer.

1×10000 (input vector) * 10000×300 matrix(W’₁₀₀₀*₃₀₀) = 1×300 vector

where W’₁₀₀₀*₃₀₀ is the weight matrix between the hidden layer and input layer

Fig 2: Word2vec neural network structure

CBOW

CBOW stands for Continuous Bag of Words. Architecture wise if we are simply explaining, CBOW is simply the lateral mirror image of the skip-gram model. Instead of predicting the context words or neighbouring words, it takes input as the context words and output the the current word wi. The number of neighbouring words to go as input go in as a input parameter. The rest of the architecture remains same. There is an input layer, hidden layer and an output layer which predicts the current word. The dimension of the hidden layer and output layer remains the same as the skip-gram model.

Lets do a dive into how the tensor dimensions sway around in the neural network.

Lets say there are C words before and after the current word taken as the context words and therefore the input will be of the size C*V, where V is the length of the one-hot encoding.

Each of these C vectors are multiplied by the weights in hidden layer which each of them would produce vectors of size 1*N, where N is hidden size dimension. Here is the representation of one of the C vector transformation at hidden layer.

Fig4: Tensor dimensional flow for CBOW neural network

Finally each of these C vectors is averaged across every word which will serve as the activation layer for the hidden layer, and this will be fed into the output layer to predict the current word.

So actually the model is getting trained on the weights between

This averaged weights learnt between the hidden layer and the output layer is the embedding of size for the current word of size (1*N), which is highlighted in purple in Fig 4.

Unlike in skip-gram model, the final embedding is the weight matrix between the hidden layer and the output layer.

When to use which?

According to the researchers, skip-gram works well with small datasets and can represent rare words. While CBOW works well with large datasets and better represent frequent words.

Implementation

We will using gensim library for basic processing of data.

import gensim
from gensim.models.callbacks import CallbackAny2Vec

// class to log the model performance at the end of the epoch
class callback(CallbackAny2Vec):
    '''Callback to print loss after each epoch.'''

    def __init__(self, reset_loss=False):
        self.epoch = 1
        self.previous_cumulative_loss = 0
        self.reset_loss = reset_loss

    def on_epoch_end(self, model):
        loss = model.get_latest_training_loss()
        if self.reset_loss:
            model.running_training_loss = 0.0
        else:
            loss_now = loss - self.previous_cumulative_loss
            self.previous_cumulative_loss = loss
            loss = loss_now

        if self.epoch % 5 == 0:
            print(f'loss after epoch {self.epoch}: {loss}')

        self.epoch += 1

// sentences_list: list sentences s
def fit(sentences_list: list, vector_size=16,
min_event_frequency=10, epochs=50, window=3):
        vector_size = vector_size
        model = gensim.models.Word2Vec(
            sentences_list,
            min_count=min_event_frequency,
            vector_size=vector_size,
            window=window,
            sg=1,
            ns_exponent=0.75,
            max_vocab_size=None,
            epochs=epochs,
            callbacks=[callback()],
            compute_loss=True
        )

        for k, v in self.model.wv.key_to_index.items():
            vectors[k] = model.wv.vectors[v]

from nltk.tokenize import word_tokenize

text_for_tokenization = \"Hi my name is Michael. \I am an enthusiastic Data Scientist. \Currently I am working on a post about NLP, more specifically about the Pre-Processing Steps."

text_for_tokenization = text_for_tokenization.split(".")
words = [word_tokenize(t) for t in text_for_tokenization]

// calling the function to fit and transform
fit(event_stream_list)

This will return a vector of dimension 300.

We could also see the nearest word in the feature space

model.wv.most_similar('computer', topn=10)

Yeah, that's it! Let's discuss more in the comment section. Until then…

Clustor

Discussion about this post